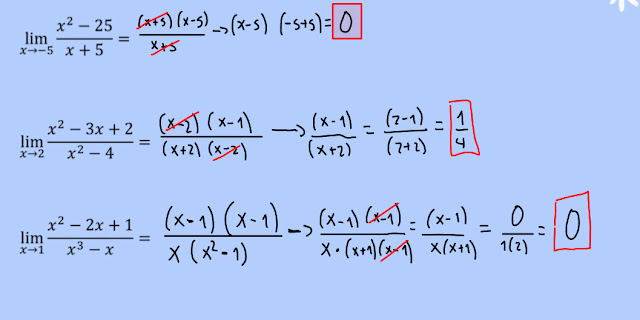Límites que involucren racionalización

Al igual que en el caso de las factorizaciones, existen indeterminaciones relacionadas con raíces, por lo que deberemos de aplicar racionalización para encontrar el límite.
Nuestro objetivo con el blog, es crear material complementario relacionado con lo visto en clases para poder ayudar a todos los estudiantes con su estudio en el electivo. Accediendo a este recurso en caso de alguna duda generada en clases, donde podrán encontrar; Apuntes, resolución de ejercicios, explicación de la materia a través de cápsulas, etc. Con el fin de lograr una mayor comprensión del electivo Límites, derivadas e integrales.