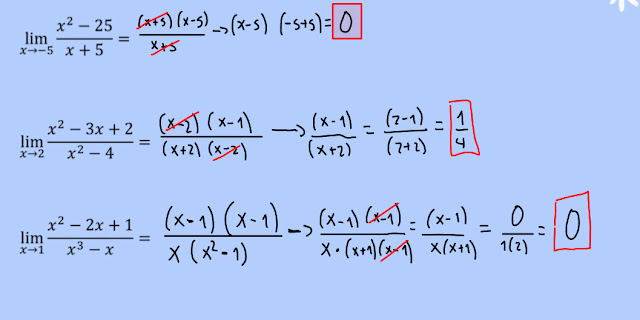Bienvenida

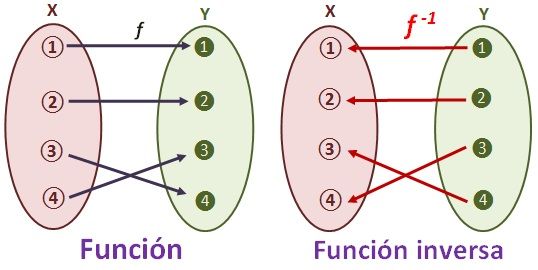
Le damos la bienvenida al blog del grupo 191, donde subiremos periódicamente contenido relacionado con el electivo: Limites, derivadas e integrales. El contenido se irá subiendo al ritmo de las clases, por lo que no estará en este blog un contenido que nunca se haya visto con antelación. El contenido estará en forma de apuntes de agradable visualización, videos explicativos; teóricos y de ejercitación. Páginas y/o videos complementarios relacionados con el material del blog. Como también trataremos de relacionar los contenidos con la Prueba de transición. Más allá de la nota que implica realizar y mantener este blog, espero que sea de ayuda para complementar las clases así mejorando las notas, como también sirva para rendir una buena prueba de transición. -Javier Barrera 4º i : Crear material audiovisual y apuntes. ...